Hilário's hobby page

Puzzles

Also see my Super Mario Maker 2 YouTube channel for videos of Super Mario levels that I made.

Hereafter I'm referring to 2D visual logic puzzles, or 'pencil puzzles'. Some brain exercises in free time.

Slant

Slant is also known as slalom, or ごきげんななめ gokigen naname in Japanese. The basic principles are very simple:

1. There is a rectangular field of contiguous squares ▢, and each square has to be filled in by one diagonal line: ⧄ ("forward slash") or ⧅ ("backward slash").
2. There is a number at the corner of some squares; the number indicates – out of the one/two/four squares that share that corner – exactly how many diagonal lines touch that corner. Corners without numbers can be touched by any number of diagonal lines.
3. The diagonal lines cannot form a loop. (The numbers do not block a continuous string of diagonals.)

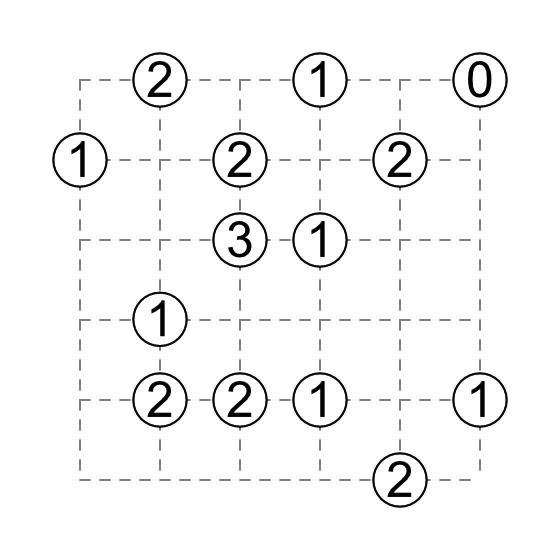
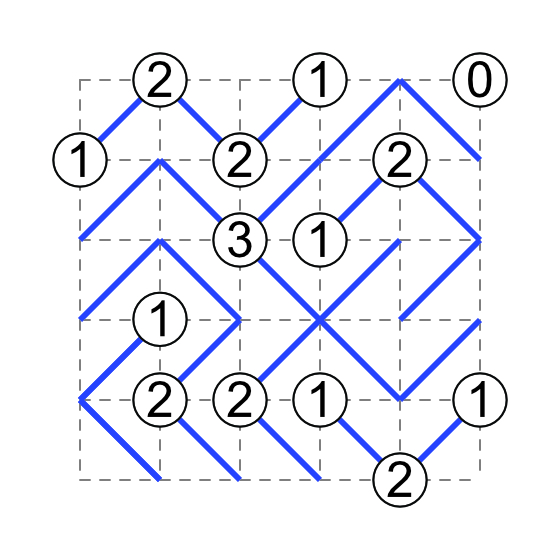
Slant is originally published by Nicoli. You can also read Nicoli's explanations of the rules in Japanese. Their English page refers the audience to the relevant English Wikipedia page.

There are many places online that you can play slant, for instance, here, here, here, [here or here (press the links which say ぱずぷれで遊ぶ next to each thumbnail to play online)].

Like other logic puzzles, you start by spotting places with unique solutions, and as you fill in the diagonals, other unique solutions/ clues will appear.

Basic logic relations

The following are the most-obvious logic relations. These, plus the no loop rule, will suffice for an easy-level puzzle. The example diagrams only show solutions in one orientation; they apply equally in other orientations. A black diagonal signifies what you have already filled in; a blue diagonal signifies what you fill in now (if that is not already filled in); a red signifies an illegal move.

Corner of field:

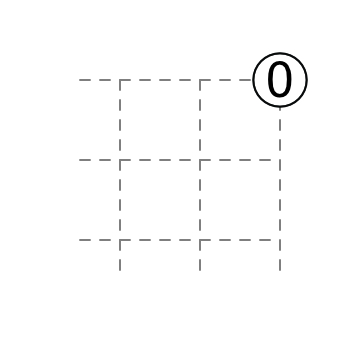
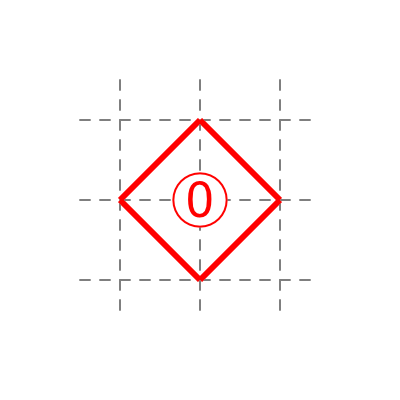
0 at corner: a diagonal does not touch the 0.

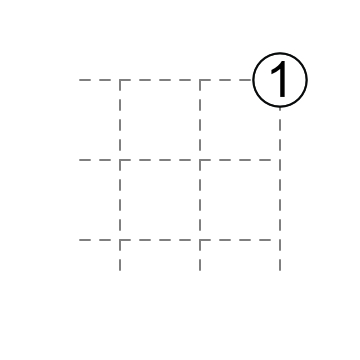
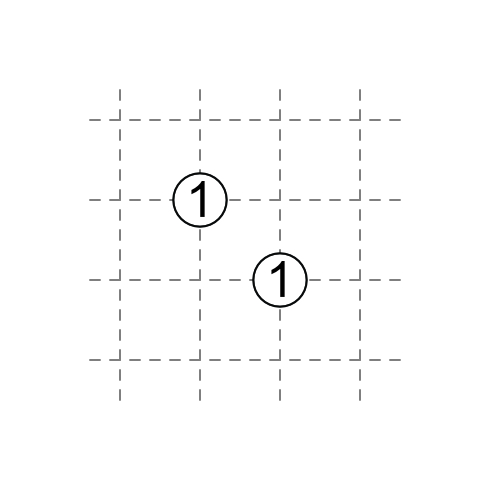
1 at corner: a diagonal touches the 1.

Edge of field:

0 at edge: neither diagonals touch the 0.

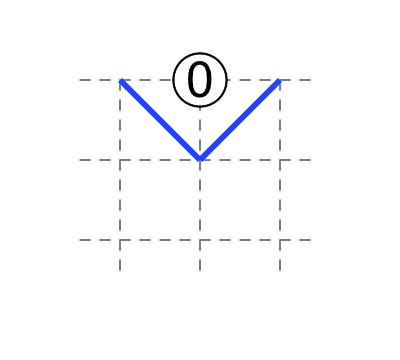
1 at edge: one diagonal touches the 1, and the other does not.

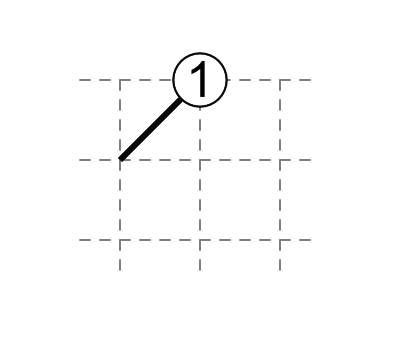
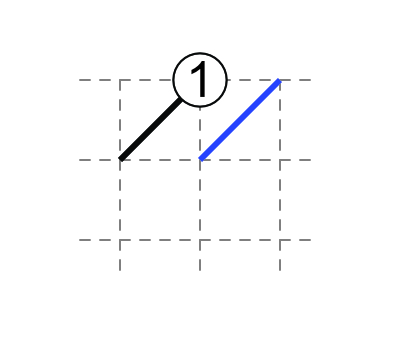
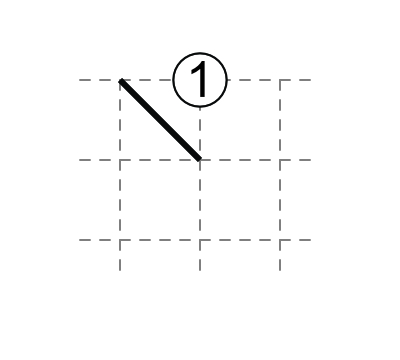
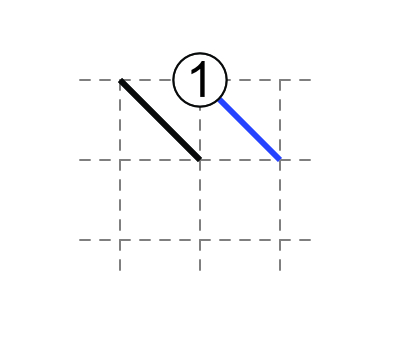
2 at edge: both diagonals touch the 2.

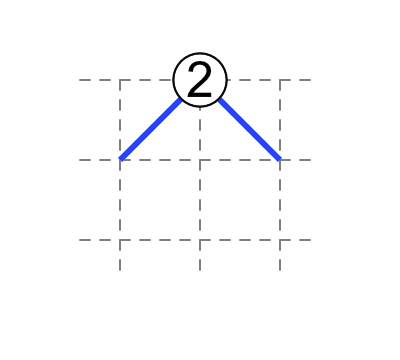
Middle of field:

0 does not occur in the middle of a field. See below.

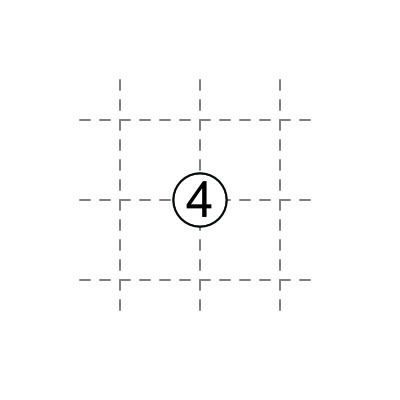
1 in middle: one diagonal touches the 1, three do not.

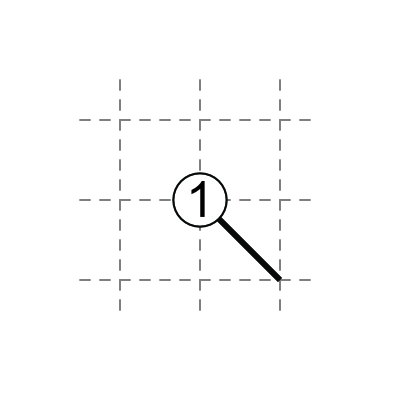
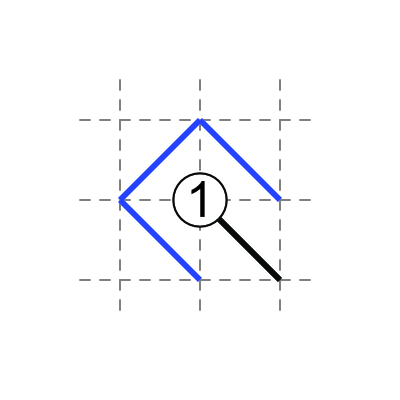
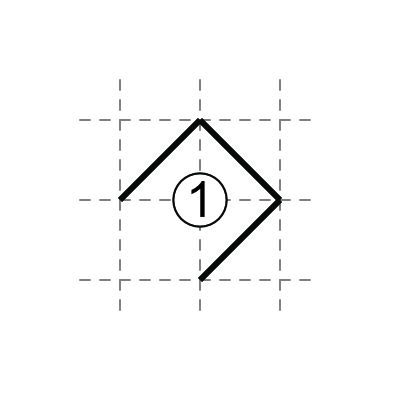
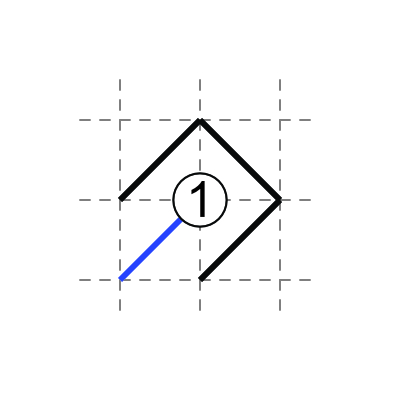
2 in middle: two diagonals touch the 2, two do not.

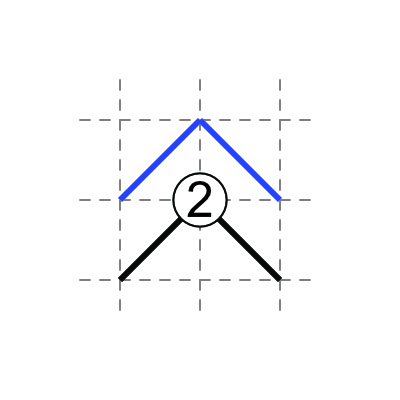
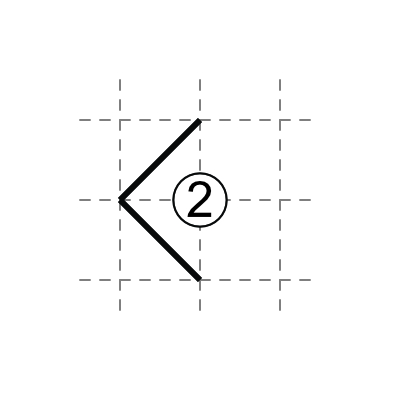
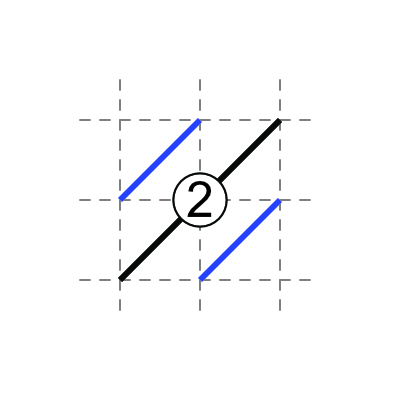
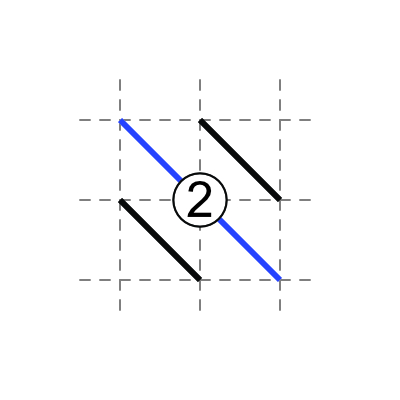
3 in middle: three diagonals touch the 3, one does not.

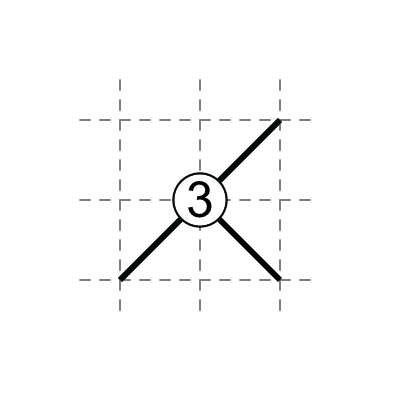
4 in middle: four diagonals touch the 4.

Logic relations between two numbers

You will need these in a hard-level puzzle. I'll leave it up to you to work out why these relations hold. Like other logic problems, check the antecedent (i.e. the 'if') and apply the consequent carefully. Avoid fallacies, which is very easy to commit, for beginners at least. If something is wrong, you have done something wrong; the following relations have been tested by a lot of people before me.

The relations outlined in this section concern two numbers orthogonally next to each other, or with an uninterrupted continuous line of 2's in between.

The relations outlined here concern the four external squares, i.e. the four squares 'facing away', and not the squares in between the two numbers concerned.

when I talk about touching/non-touching diagonals, I em refering to diagonals touching or not touching the number, not diagonals touching or not touching other diagonals. By default I am talking about numbers in the middle of a field, unless I specify that a number is on the edge.

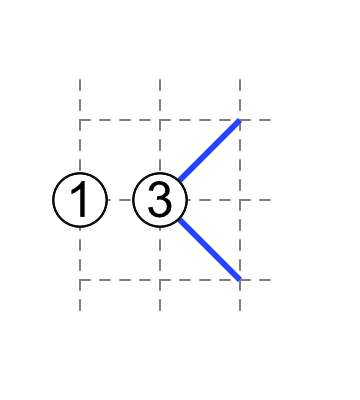
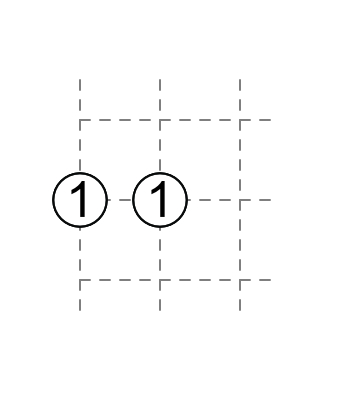
1–1

The 1's have non-touching external diagonals.

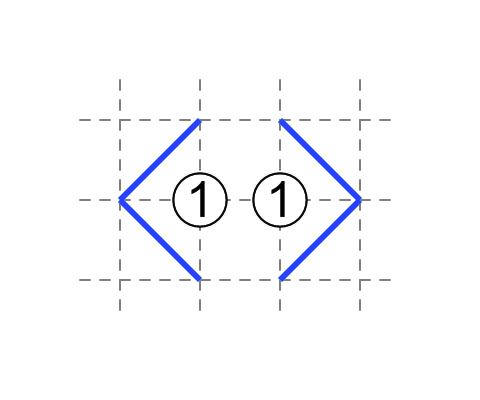
Here and below, you will notice that a number on the edge behaves like a number with non-touching external diagonals. When a 1 is on the edge and a 1 is in the middle of a field, the 1 in the middle of a field has non-touching external diagonals.

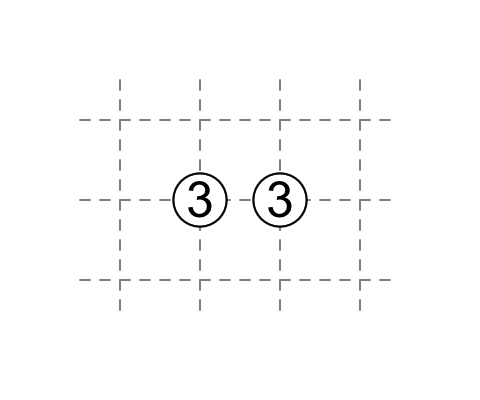
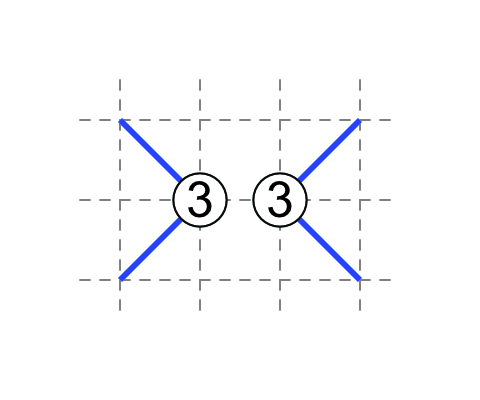
3-3

The 3's have touching external diagonals.

1-3

If 1 has non-touching external diagonals, then 3 has touching external diagonals.

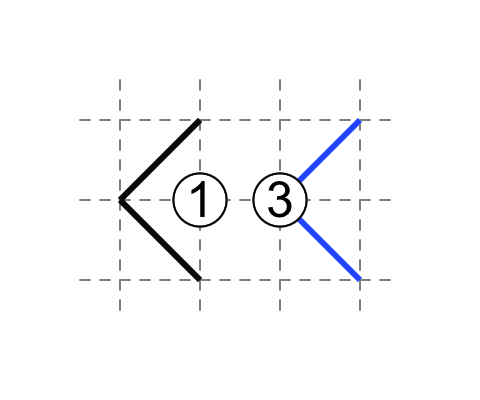
Analogously when you have a 1 on the edge.

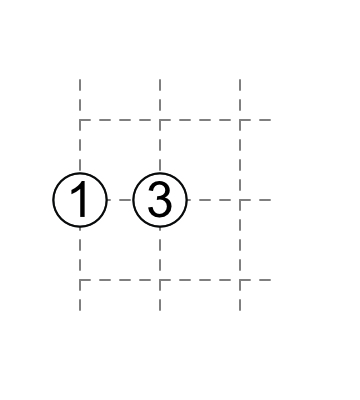
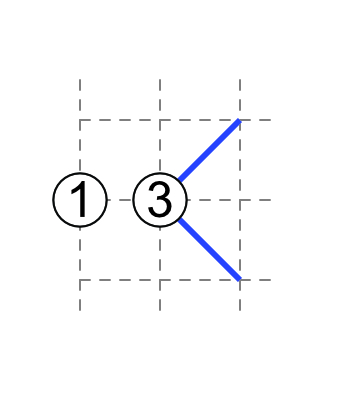
If 3 has touching external diagonals, then 1 has non-touching external diagonals.

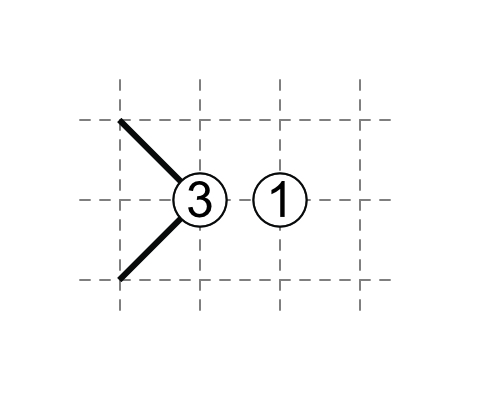
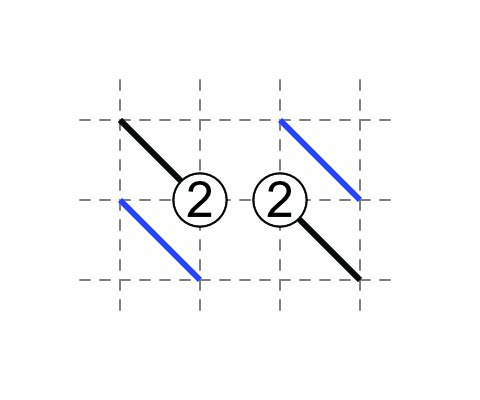
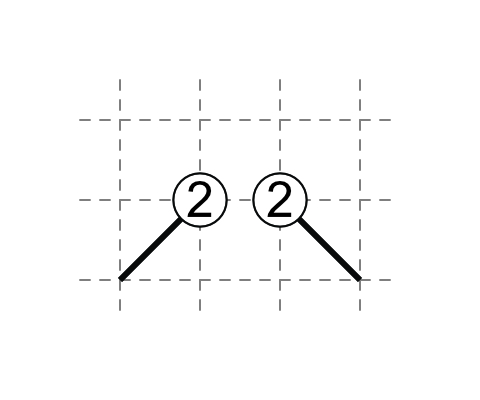
2-2

If each 2 has one touching external diagonal, then each 2 has one non-touching diagonal.

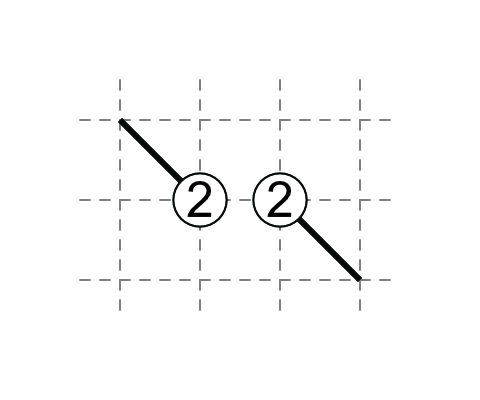
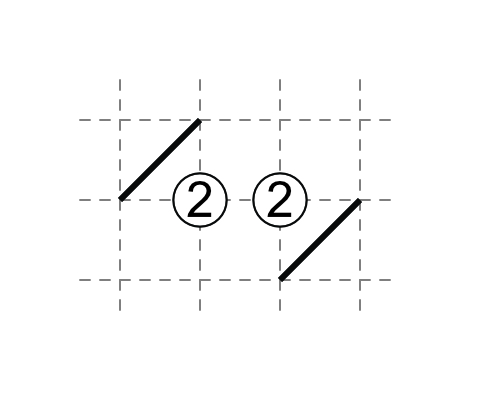
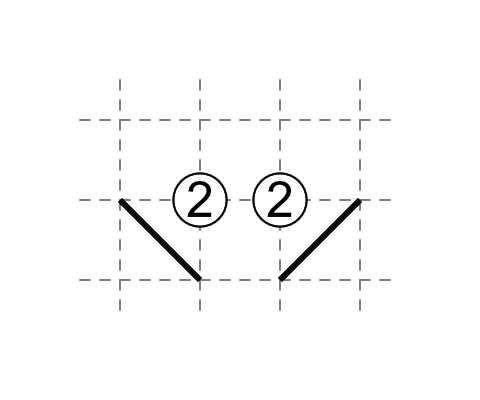
If each 2 has one non-touching external diagonal, then each 2 has one touching diagonal.

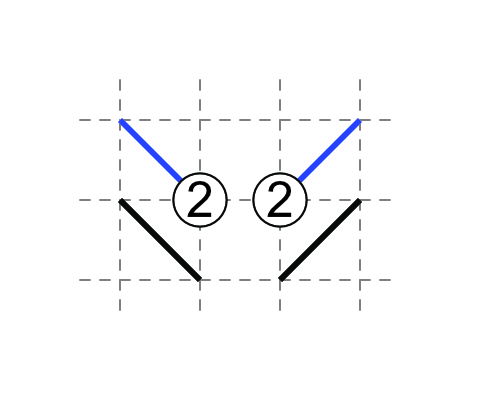
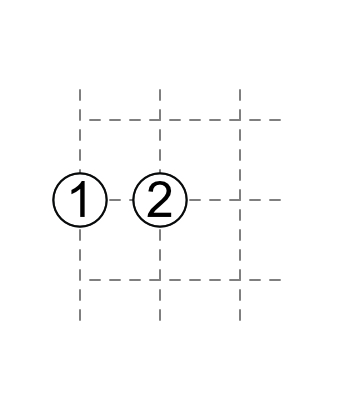
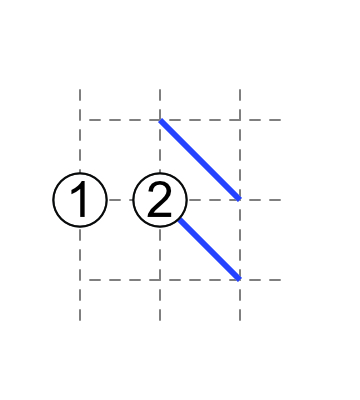
2-1

If 2 has one touching external diagonal, the the other three external diagonals are non-touching.

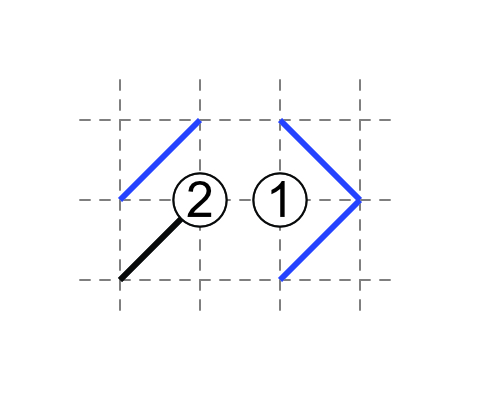
If 1 has non-touching external diagonals, then 2 has parallel external diagonals. (You will need clues elsewhere to know the orientation of one of the two diagonals first.)

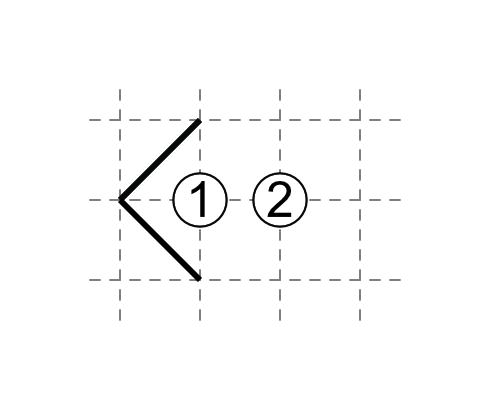
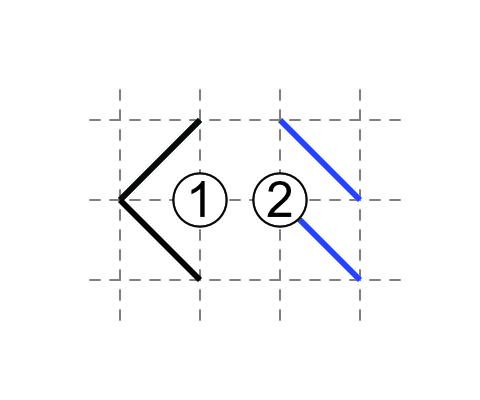
Analogously when you have a 1 on the edge.

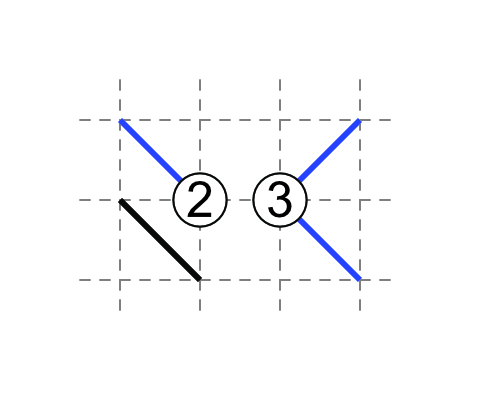
2-3

If 2 has one non-touching external diagonal, then the other three external diagonals are touching.

If 3 has touching external diagonals, then 2 has parallel external diagonals. (You will need clues elsewhere to know the orientation of one of the two diagonals first.)

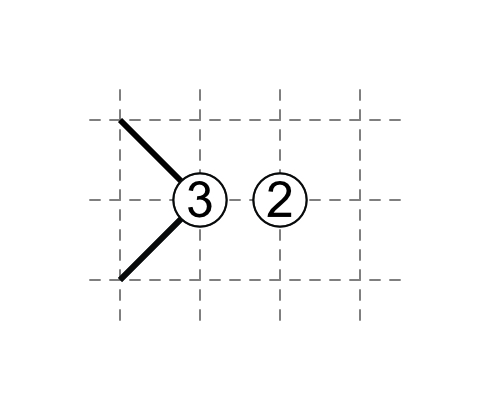
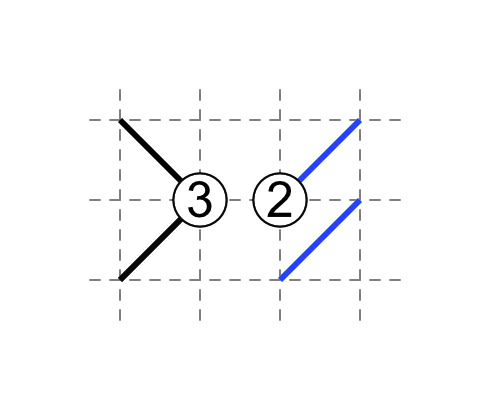
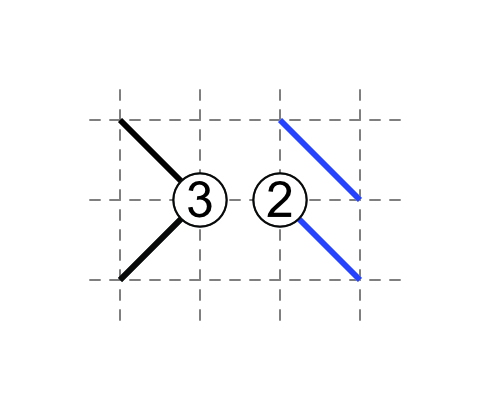
Not forming loops

A 0 does not exist in in the middle of a field; having so would form a rhombus (i.e. a loop) around it.

For two 1's diagonally next to each other, and neither is on the edge, then the diagonal in the square between them do not touch the 1's.

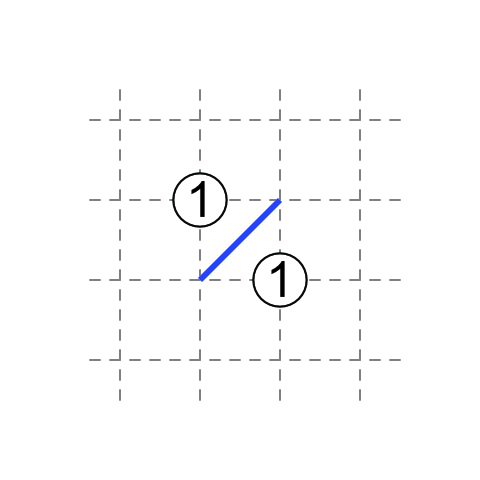
Because if the diagonal touches the two 1's, a loop will form around it.

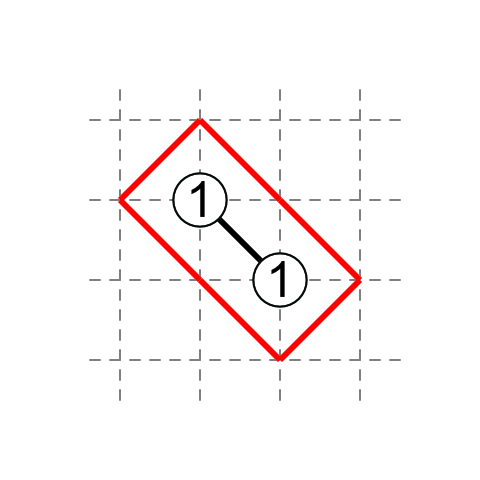
When there is a string of diagonals that is one diagonal away from forming a loop, the remaining square has a diagonal in an orientation that prevents that loop from forming. The following is the simplest example.

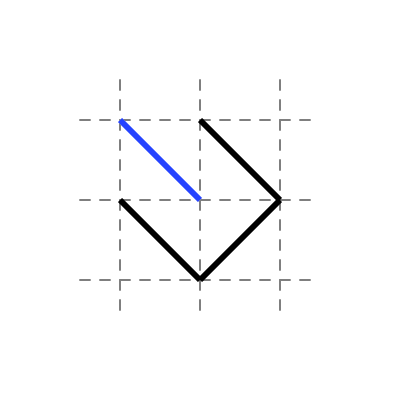
The following is another example.

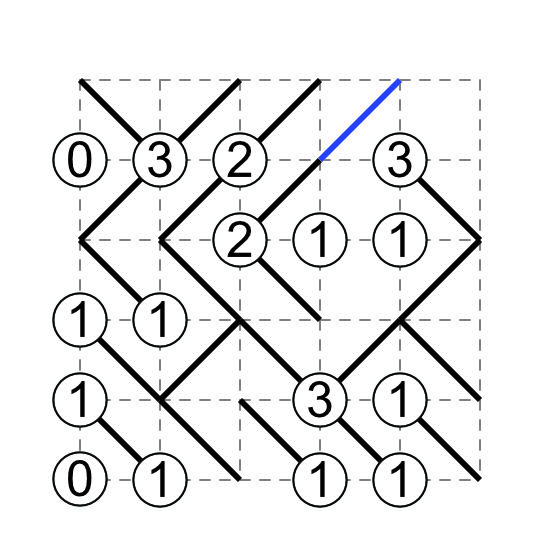
Larger loops are harder to spot. Often an easier way is to spot diagonal networks that would be 'trapped' by such loops. All diagonals form paths that eventually reach the edge of the field. If all ends of a diagonal path network are dead-ends in the middle of a field, a loop will form around it, and that has to be avoided. The following is a simplified example. The string of diagonals with the numbers 1–3–1 all lead to a dead-end, except at the 3; the string of diagonals must have an outlet.

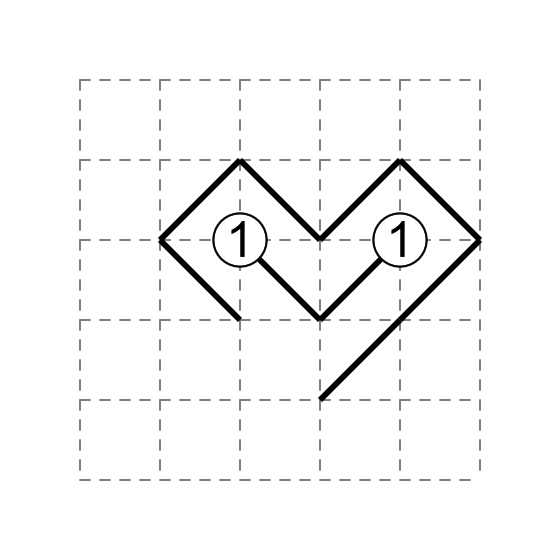
Especially useful is to spot a diagonal that might lead to a 1 in the middle of a field (i.e. not on the edge). A diagonal that leads to a 1 is a sure dead-end; if all the other ends of the diagonal network are already deadends, the last diagonal must not lead to a 1 in the middle of a field. In the following simplified example, the only outlet of the diagonal network is with the 2 on the left; if the remaining diagonal of the 2 leads to either of the 1's, the entire network would be trapped by a loop. Therefore, the remaining diagonal of the 2 leads to bottom-left corner with no number.

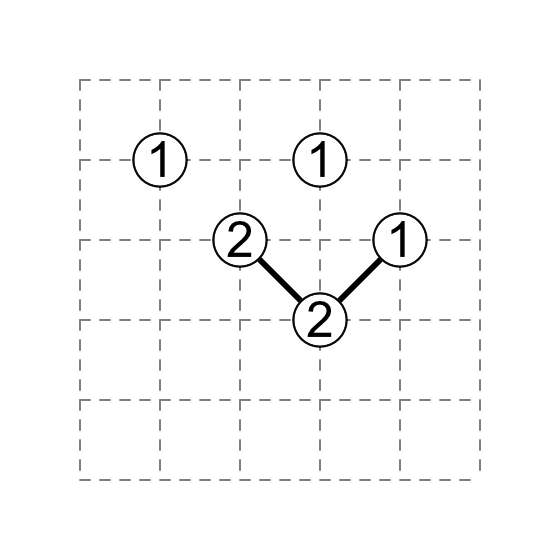
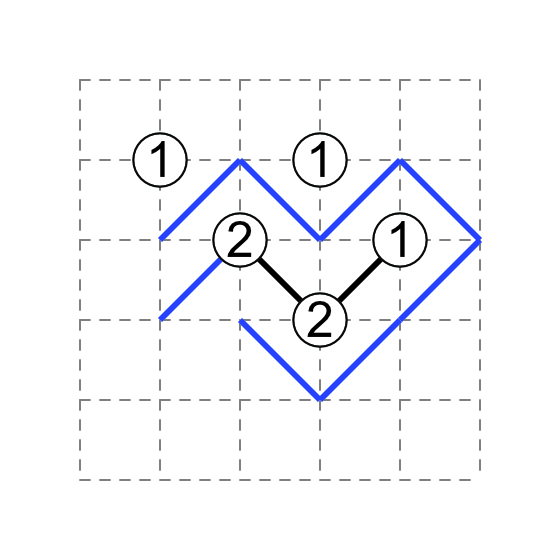
Sources

I learnt a lot from this and this (pg. 1, 2, 3). Sehr gut.

There are yet other tricks to discover. Happy discovering them by playing more slant puzzles!